Calculation of Winkler-Pasternak Constants from Deformation Parameters of Soils
The Winkler - Pasternak constants C1 and C2 are calculated in the program from the condition of equal flexibility matrices of infinitely stiff infinite strip footing resting on the Winkler - Pasternak and elastic subsoil.
The layer material is characterized by the following quantities:
Edef | - | deformation modulus [MPa] |
ν | - | Poisson's ratio |
Eoed | - | oedometric modulus [MPa] |
G | - | shear modulus [MPa] |
Of these, Edef and ν are independent, the other two are determined by relations:
![]()
and
![]()
The strip footing has a width of 2b and the deformation zone under the strip has a thickness of H.
By the solution of the elastic subgrade we mean finding the relationship between the displacement and the load of the strip footing in the form:
![]()
where P is the flexibility matrix.
By solving for an isotropic homogeneous elastic layer under the foundation waist while avoiding horizontal displacements, we obtain a flexibility matrix P of the form:

where
![]()
and
![]()
By solving the differential equation for the two-parameter subsoil model, we obtain a matrix P of the form:
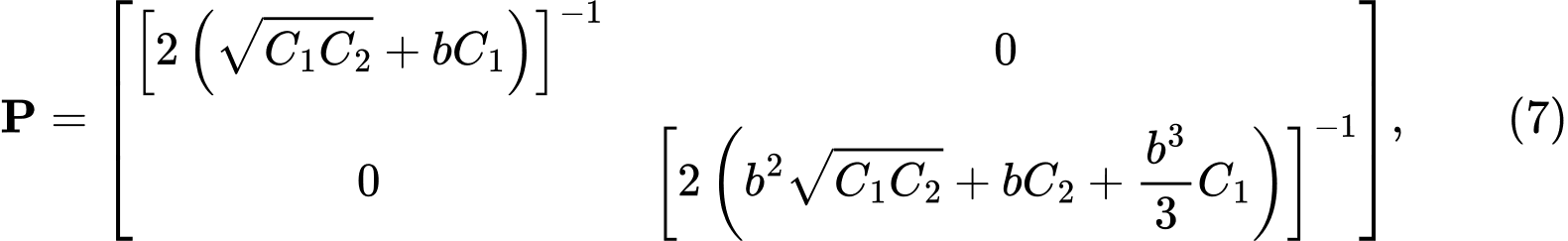
where C1, C2 are the constants of the Winkler-Pasternak subsoil model. We find their values from the condition that the matrix P of expression (4) must be identical to the matrix P of expression (7). By comparison and modification we obtain the relations:
![]()
and
![]()
where

and
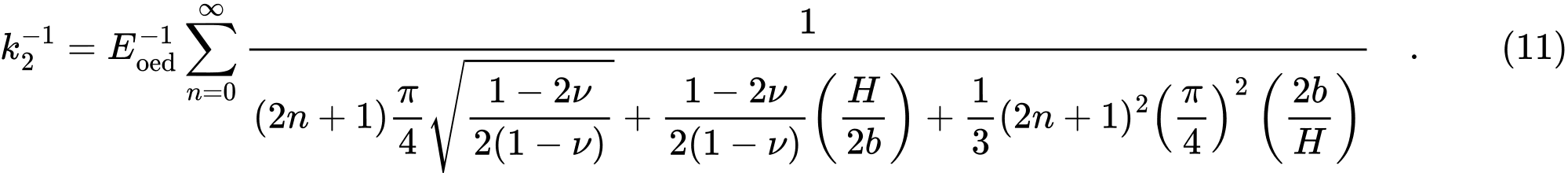
From relations (8) and (9), the values of C1 and C2, are directly calculated, while the infinite sums in expressions (10) and (11) are performed in Geo5 for the first 21 addends.
Literature: Kuklík, P.: Příspěvek k řešení vrstevnatého podloží, Pozemní stavby, 7-1984