Modèles d'état critique
Les modèles d'état critique reposent sur le concept d'un état d'indice des vides critique auquel une déformation par cisaillement illimitée peut avoir lieu sans modifier la contrainte moyenne courante et l'indice des vides correspondant (déformation volumétrique).
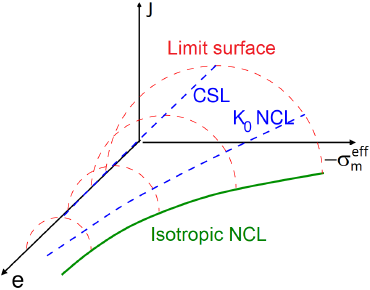
Ces modèles s'avéreront particulièrement utiles dans les tâches où la prévision du tassement joue un rôle important. Ils capturent un certain nombre de propriétés du sol, qui peuvent difficilement être traitées par des modèles de plasticité simplifiés, y compris la rigidité dépendant de la contrainte, la réponse du sol dépendant de la porosité, le comportement non linéaire à l'intérieur de la surface de charge, la prévision de la dilatance et de l'état critique limite sans introduire indépendamment l'angle de dilatance, la possibilité de définir une surface limite (surface limite d'état) dans l'espace de la contrainte et de la porosité, cf. la figure ci-dessous, où CSL représente la ligne d'état critique, NCL désigne le sol normalement consolidé en supposant une consolidation K0 (K0 = K0NC, où K0NC est le coefficient de pression latérale au repos d'un sol normalement consolidé) ou une consolidation isotrope (K0 = 1), e est l'indice des vides, σm est la contrainte moyenne et J est la mesure équivalente du vecteur des composantes déviatoriques de la contrainte.
La classe des modèles d'état critique comprend les modèles Cam-clay modifié, de Cam-clay généralisé et d'argile hypoplastique. Les modèles basés sur la théorie de la plasticité appartiennent également au groupe des modèles de matériaux élastiques-plastiques avec durcissement et adoucissement.