Cálculo das Constantes de Winkler-Pasternak a partir dos Parâmetros de Deformação dos Solos
As constantes de Winkler-Pasternak C1 e C2 são calculadas a partir da condição da matriz de igual conformidade de uma fundação contínua infinitamente rígida assente num subsolo elástico de Winkler-Pasternak.
Esta condição é representada pelos seguintes parâmetros:
Edef | - | módulo de deformução [MPa] |
ν | - | coeficiente de Poisson |
Eoed | - | módulo edométrico [MPa] |
G | - | shear modulus [MPa] |
Destes, Edef e ν são independenetes, enquanto que os outros são obtidos através das seguintes relações:
![]()
e
![]()
A fundação contínua tem uma largura de 2b e a zona de deformação abaixo da fundação tem uma espessura de H.
Através da solução do gradiente elástico, é possível obter a relação entre o deslocamento e a carga da fundação contínua:
![]()
onde P é a matriz de flexibilidade.
Ao resolver a equação para uma camada isotrópica homogénea elástica abaixo da fundação, sem deslocamentos horizontais, obtemos a matriz de flexibilidade P com a forma:
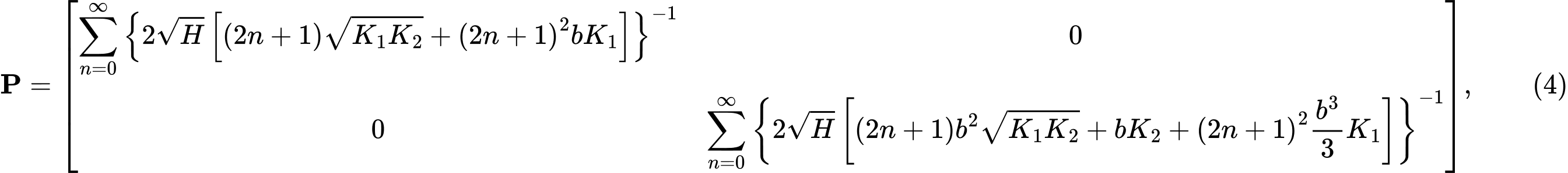
onde
![]()
e
![]()
Ao resolver a equação diferencial para o modelo do subsolo de dois parâmetros, obtemos a matriz P com a forma:
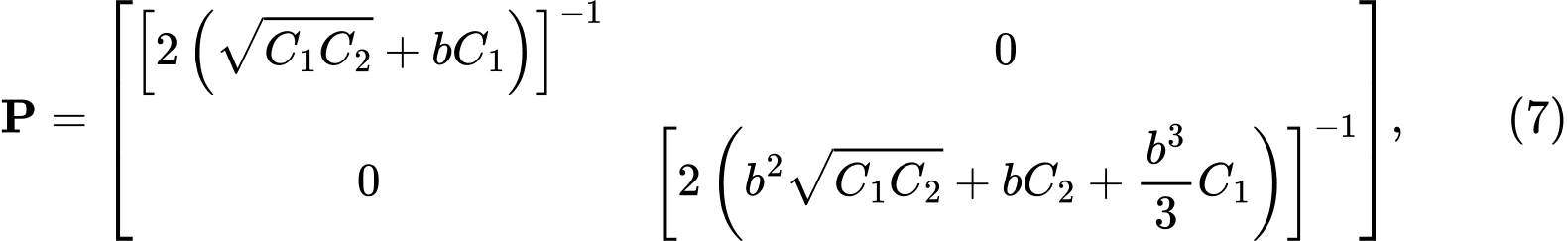
onde C1, C2 as são constantes do modelo do subsolo de Winkler-Pasternak. Obtemos os seus valores a partir da condição em que a matriz P da expressão (4) deve ser idêntica à da matriz P da expressão (7). Ao comparar e modificar as equações obtemos as seguintes relações:
![]()
e
![]()
onde
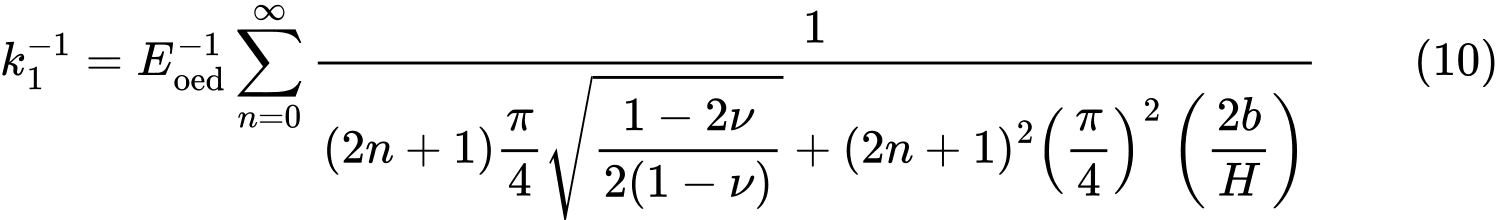
e
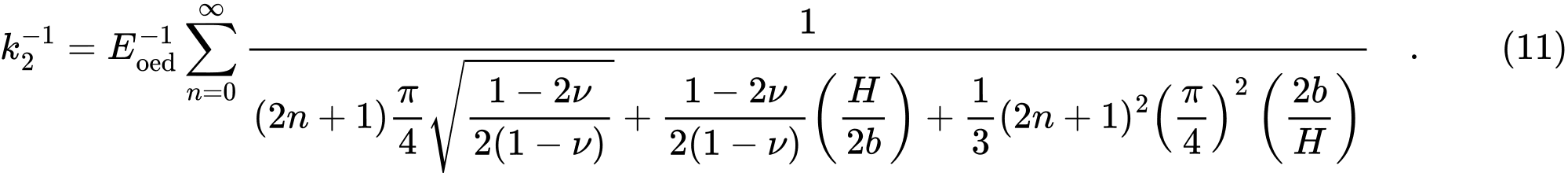
A partir das relações (8) e (9), os valores de C1 e C2, são diretamente calculados, enquanto que os somatórios infinitos das expressões (10) e (11) são realizados no GEO5, para as primeiras 21 iterações.
Bibliografia:
Kuklík, P.: Příspěvek k řešení vrstevnatého podloží, Pozemní stavby, 7-1984