Endurecimento do Solo
O modelo de Endurecimento do solo, desenvolvido por Schanz et al. [1], é adequado à modelação de vários solos moles. O modelo combina dois mecanismos de endurecimento. O mecanismo de endurecimento devido ao cisalhamento define o desenvolvimento de deformações plásticas causadas por componentes de tensão de desvio, enquanto que o mecanismo devido à compressão torna-se ativo durante o modo compressivo do carregamento, por exemplo, em compressão edométrica ou isotrópica. O mecanismo devido ao cisalhamento é manifestado por um desenvolvimento gradual da superfície de cedência de cisalhamento fsHS em função do valor atual da deformação plástica equivalente de desvio κs (ou γps).
Este processo de endurecimento (expansão da superfície de cedência) é acompanhado pela evolução do ângulo de atrito interno mobilizado φm e termina ao atingir a superfície de cedência de cisalhamento limite fsMN. No GEO5 MEF, esta função de cedência é apresentada na forma do critério de cedência de Matsuoka-Nakai em função dos valores de pico dos parâmetros de resistência de cisalhamento, a coesão c e o ângulo de atrito interno φ. A projeção da superfície de cedência no plano de desvio tem a forma de uma curva convexa suave que atravessa todos os vértices do modelo de Mohr-Coulomb. A consequência do endurecimento devido à compressão é o desenvolvimento da superfície de cedência fcHS em função da evolução da pressão de pré-consolidação pc. Também foi apresentada uma formulação semelhante para medidas de tensão invariável em [2].
A figura seguinte apresenta uma representação gráfica de ambas as superfícies de cedência. É possível observar o desenvolvimento gradual da superfície de cedência de cisalhamento, na projeção da superfície de cisalhamento no plano meridiano. O modelo de Relaxamento do solo é definido de forma semelhante mas, no entanto, apenas implementa a superfície de cisalhamento limite. O endurecimento fica, assim, limitado à compressão.
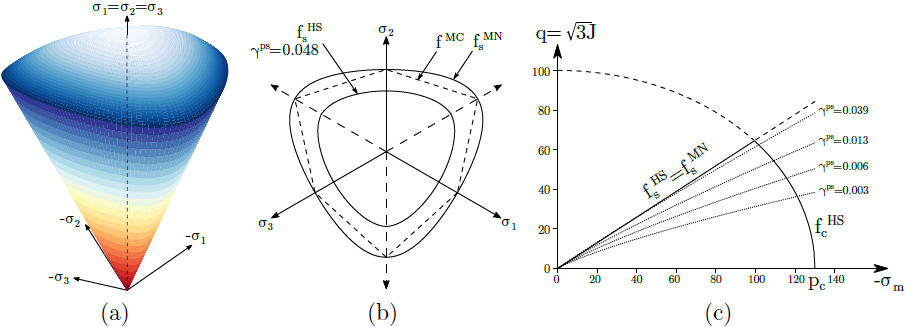 a) superfície de cedência no espaço de tensão principal, b) projeção no plano de desvio e principal e c) no plano meridiano
a) superfície de cedência no espaço de tensão principal, b) projeção no plano de desvio e principal e c) no plano meridiano
A formulação da superfície de cedência de cisalhamento vem do pressuposto de que a relação entre a tensão de desvio q e a deformação vertical ε3 durante um ensaio triaxial drenado podem ser descrita através de uma função hiperbólica. A figura seguinte mostra o diagrama tensão-deformação correspondente, onde qa corresponde ao valor da assintota de q e qfMC corresponde ao valore de q quando se atinge a superfície limite, para a qual qf = Rfqa, onde Rf corresponde ao coeficiente de redução. Pode encontrar mais detalhes no manual teórico.
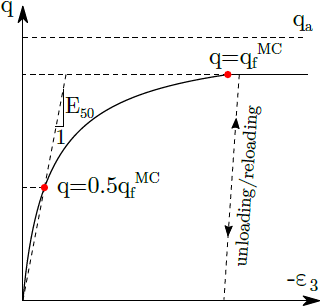 Lei de tensão-deformação hiperbólica
Lei de tensão-deformação hiperbólica
A tabela seguinte resume os parâmetros do modelo material de Endurecimento do solo.
Símbolo | Unidade | Descrição | |
| [MPa] | Módulo secante de elasticidade | |
| [MPa] | Módulo de relaxamento/recarregamento | |
| [-] | Coeficiente de Poisson | |
| [kPa] | Tensão média de referência | |
| [-] | Exponente da lei de rigidez | |
| [kPa] | Valor limite da tensão média para assegurar uma rigidez não nula | |
| [kN/m3] | Peso volúmico | |
| [-] | Índice de vazios inicial, correspondente ao estado do final da 1a etapa de cálculo | |
| [-] | Rácio de cedência | |
| [kPa] | Coesão efetiva de pico | |
| [°] | Ângulo de atrito interno efetivo de pico | |
| [°] | Ângulo de dilatação | |
| Peso volúmico | ||
| [-] | Coeficiente de empuxo de terra lateral em repouso de solo normalmente consolidado | |
| [MPa] | Módulo edométrico tangente | |
| [kPa] | Tensão vertical de referência para determinar | |
| [-] | Índice de vazios máximo para terminar a dilatação (ao limitar a dilatação) | |
| [-] | Rácio de sobre-consolidação | |
| [kPa] | Pressão de pré-consolidação | |
| [1/K] | Coeficiente de dilatação térmica (ao considerar efeitos de temperatura) | |
| [-] | Parâmetro para definir a forma da prensa | |
| [Pa] | Módulo de endurecimento (não introduzido) | |
| [kPa] | Pressão de pré-consolidação | |
| [°] | Ângulo de atrito em estado crítico (não introduzido) | |
| [°] | Ângulo de atrito interno mobilizado (não introduzido) | |
| [°] | Ângulo de dilatação mobilizado (não introduzido) |
O módulo secante de elasticidade Eip,ref pode ser obtido por aproximação em função do módulo de elasticidade E50p,ref de acordo com
![]()
onde o índice (p,ref) representa um valor de referência do módulo para um dado valor de referência da tensão média efetiva σmref. O modelo assume a evolução do módulo de elasticidade como função da tensão média atual, de acordo com
![]()
De notar que esta formulação difere da utilizada nas publicações [1] e [2], por exemplo, em que a evolução da rigidez dependo da tensão principal mínima σ1. Tal deve ser levado em consideração ao adotar parâmetros de calibração de outro software de engenharia para utilizá-los no programa GEO5 MEF. è possível recorrer a um conjunto de parâmetros modificados que permitam atingir uma correspondência de simulações entre programas. Para tal, o recurso a uma regressão linear simples será suficiente para ajustar os parâmetros Eurp,ref e mp. A figura seguinte ilustra um exemplo desta aplicação.
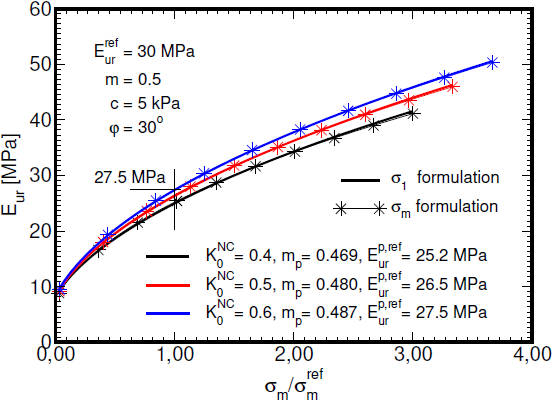 Determinação da dependência do módulo de relaxamento/recarregamento Eur na tensão média σm através de uma regressão linear
Determinação da dependência do módulo de relaxamento/recarregamento Eur na tensão média σm através de uma regressão linear
Os parâmetros modificados E50p,ref(Eip,ref) e Rf podem ser obtidos, consequentemente, através de um otimização pela comparação de simulações numéricas de um ensaio de compressão triaxial, para os parâmetros já determinados Eurp,ref e mp.
Pode encontrar mais detalhes no manual teórico. No entanto, é expressamente recomendável, que para calibrar parâmetros específicos do modelo, com base em ensaios laboratoriais, se recorra a um software de calibração como o ExCalibre, por exemplo.
A prensa de compressão fcHS é determinada pelo parâmetro M que se refere à sua forma e pelo módulo de endurecimento H em função do aumento da pressão de pré-consolidação Δpc dado o aumento da deformação plástica volumétrica Δεvpl. O módulo de endurecimento H é dado por
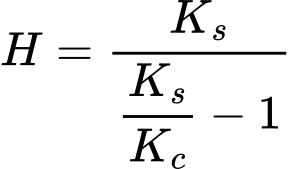
onde Kc, Ks são módulos de dilatação para o carregamento inicial e relaxamento, respetivamente. Pode encontrar mais detalhes no manual teórico. Os parâmetros ![]() podem ser inseridos diretamente ou determinados automaticamente com base nos valores do coeficiente de empuxo de terra lateral em repouso para solos normalmente consolidados K0NC e do módulo edométrico Eoedref. Isto é obtido através da otimização numérica de ensaio laboratorial edométrico. O objetivo é determinar os parâmetros do modelo M, H de forma a que o módulo edométrico estimado numericamente esteja de acordo para o definido para o valor de K0NC como mostra a figura seguinte. A tensão média σm* e a tensão de desvio equivalente J* são dadas por
podem ser inseridos diretamente ou determinados automaticamente com base nos valores do coeficiente de empuxo de terra lateral em repouso para solos normalmente consolidados K0NC e do módulo edométrico Eoedref. Isto é obtido através da otimização numérica de ensaio laboratorial edométrico. O objetivo é determinar os parâmetros do modelo M, H de forma a que o módulo edométrico estimado numericamente esteja de acordo para o definido para o valor de K0NC como mostra a figura seguinte. A tensão média σm* e a tensão de desvio equivalente J* são dadas por
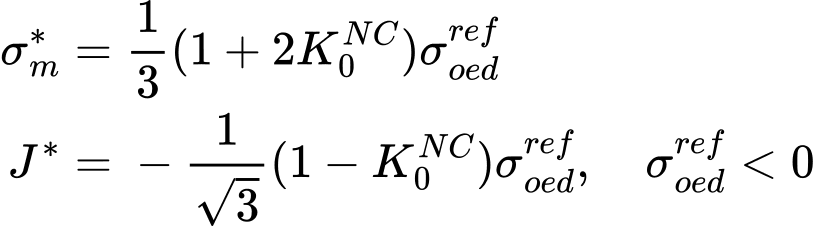
Pode encontrar mais detalhes no manual teórico.
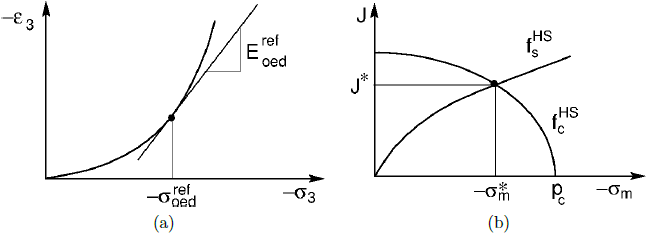 a) representação gráfica do módulo edométrico de referência Eoedref para o ponto correspondente ao σoedref definido, b) tensão atual no final da otimização para σoedref
a) representação gráfica do módulo edométrico de referência Eoedref para o ponto correspondente ao σoedref definido, b) tensão atual no final da otimização para σoedref
O modelo de endurecimento do solo permite modelar a dilatação (desenvolvimento de deformações plásticas volumétricas durante o cisalhamento plástico) considerando o ângulo de dilatação ψ. O desenvolvimento de deformações plásticas deve-se ao potencial plástico gsHS. A definição do potencial plástico é semelhante à adotada para o modelo de Drucker-Prager. A única diferença é na definição da inclinação do potencial plástico Mψ que passa a depender do valor atual do ângulo de atrito interno mobilizado ψm. A equação correspondente é formulada de forma semelhante ao do modelo de Mohr-Coulomb Modificado, para a teoria de dilatação de Rowe.
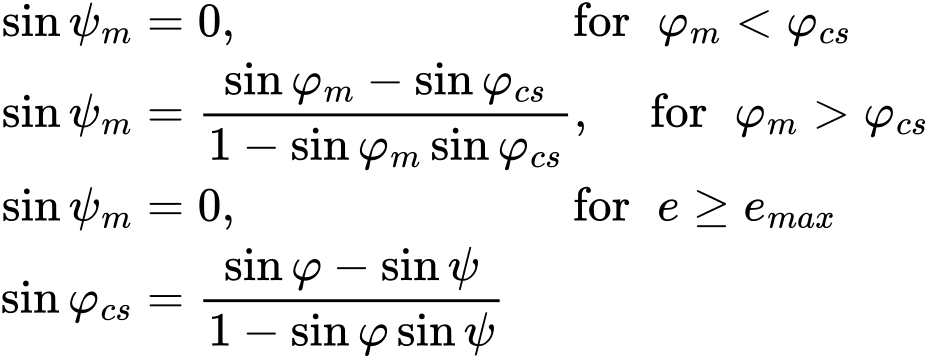
onde φ, φm, φcs, ψ correspondem ao ângulo de atrito interno de pico, ao ângulo de atrito interno mobilizado, ao ângulo de atrito em estado crítico e o ângulo de dilatação de pico. A figura seguinte mostra a representação gráfica da evolução de ψm. A figura também mostra um corte da dilatação potencial através da definição do índice de vazios máximo emax, para o qual se espera atingir o estado crítico em que ψm = 0.
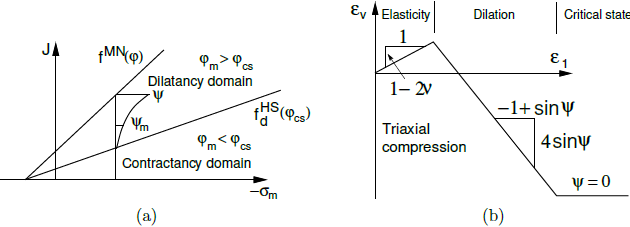 Teoria de dilatação de Rowe: a) representação gráfica doa evolução do ângulo de dilatação mobilizado ψm, b) corte na dilatação
Teoria de dilatação de Rowe: a) representação gráfica doa evolução do ângulo de dilatação mobilizado ψm, b) corte na dilatação
A evolução da rigidez depende do valor atual da tensão média efetiva σm. Tal está relacionado com a seleção da etapa inicial de carregamento, que implica valores muito reduzidos para que a tensão inicial seja suficientemente reduzida. De forma a acelerar a convergência, é adequado explorar o número mínimo de iterações para uma única etapa de carregamento. A influência da magnitude da etapa inicial de carregamento na evolução da tensão e da deformação está descrita em detalhe aqui.
Uma etapa importante para obter uma análise bem sucedida é a definição dos valores iniciais da tensão de pré-consolidação pcin e da deformação plástica de desvio equivalente κsin. Ambos os parâmetros dependem do estado atual de tensão para o momento em que o modelo de endurecimento do solo é introduzido na análise, de forma a que o estado de tensão atual satisfaça tanto as funções de cisalhamento e de cedência. Pode encontrar mais detalhes aqui. Também é possível consultar a descrição dada para o modelo de Cam clay Modificado.
O modelo permite ajustar o valor inicial da pressão de pré-consolidação em função do grau de pré-consolidação esperado, através dos parâmetros ![]() e
e ![]() . Pode encontrar mais detalhes aqui. De notar que esta opção apenas está disponível ao definir a tensão geostática inicial com recurso ao procedimento K0.
. Pode encontrar mais detalhes aqui. De notar que esta opção apenas está disponível ao definir a tensão geostática inicial com recurso ao procedimento K0.
No caso de a análise implicar condições não drenadas, é possível recorrer apenas ao Tipo (1): análise para tensão efetiva (cef, φe).
O modelo de endurecimento do solo também permite realizar análises de estabilidade. No entanto, esta opção apenas está disponível ao executar a análise de estabilidade dentro da etapa de construção respetiva. Neste caso, a prensa de compressão e a evolução do ângulo de atrito mobilizado são desativados de forma semelhante. Assim, apenas fica ativa a superfície de cedência limite fsMN. O problema é resolvido de forma gradual, reduzindo os parâmetros de resistência ao cisalhamento de pico c, φ de forma idêntica ao descrito para o modelo de Drucker-Prager.
A performance do modelo em ensaios laboratoriais é examinada aqui, incluindo a influência da magnitude da etapa de carregamento inicial.
A menos que exista evidência experimental clara de valores diferentes, os parâmetros do modelo de endurecimento do solo devem corresponder aos valores de referência listados na tabela seguintes.
Símbolo | Unidade | Valor de Referência | |
| [MPa] | (2, 70) | |
| [MPa] |
| |
| [kPa] | 100.0 | |
| [-] | (0.3, 0.9) | |
| [kPa] | 10.0 | |
| [-] | 0.9 | |
| [°] | (16.0, 42.0) | |
| [kPa] | (0.0, 50.0) | |
| [°] |
| |
| [-] | (0.5, 2.5) | |
| [-] | 0,2 | |
| [-] |
| |
| [-] |
| |
| [kPa] | 100.0 | |
| [MPa] |
|
A implementação do modelo de endurecimento do solo no programa GEO5 MEF está descrito com detalhe no manual teórico.
Bibliografia:
[1] T. Schanz, P.A. Vermeer, P.G. Bonnier, The hardening soil model: Formulation and verification, Beyond 2000 in Computational Geotechnics, Balkema, Rotterdam. 1999
[2] T. Benz, Small-Strain Stiffness of Soils and its Numerical Consequences, PhD thesis, University of Stuttgart, 2007