Tensão Invariável e Medidas de Deformação

A tensão invariável e as medidas de deformação permite descrever um estado tridimensional de tensão através de quantidades escalares, invariáveis. Um valor invariável é um valor que não depende do sistema de coordenadas definido. Assim, pode ser expresso através das variáveis definidas no sistema de coordenadas cartesiano base como das variáveis associadas ao sistema de coordenadas principal, adotando as tensões e deformações principais. De notar que as tensões principais também podem ser definidas como invariáveis. Para além de permitirem uma representação gráfica simples do estado de tensão tridimensional, estas variáveis também são utilizadas para a formulação da maioria das superfícies de cedência.

Apresenta-se uma lista de tensões invariáveis e medidas de deformação, para o caso da compressão triaxial definida em função das tensões e deformações principais. Pode encontrar mais detalhes no manual teórico.

• Tensão média

• Deformação volumétrica

• Tensão de desvio equivalente

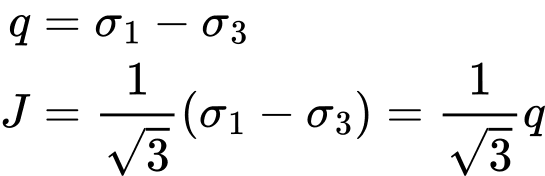
• Deformação de desvio equivalente

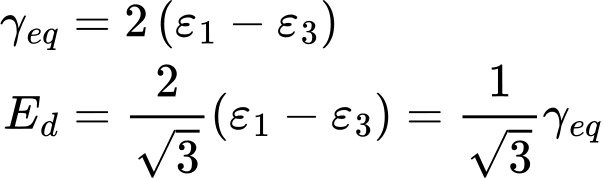
• Expressão genérica do Ângulo de Lode (para compressão triaxial, aplica-se σ₂ - σ₃ = σ₁ - σ₃ 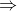θ = 30°)