软化和硬化
标准的Drucker-Prager和修正Mohr-Coulomb方程描述了当岩土材料强度参数c和φ在分析中保持不变时弹塑性和刚塑性岩土材料的应力应变行为。这两个模型的增强版(勾选高级选项)允许这些强度参数作为等效塑性偏应变的函数:
![]()
![]()
其中: |
| - | 等效塑性偏应变,由下式计算: |
![]()
![]()
![]()
其中: |
| - | 等效塑性偏应变 |
| - | 塑性偏应变张量 | |
| - | 塑性应变张量 | |
| - | 塑性体积应变 | |
| - | Kronecke符号 |
强度参数变量的分段线性假定如下图所示。
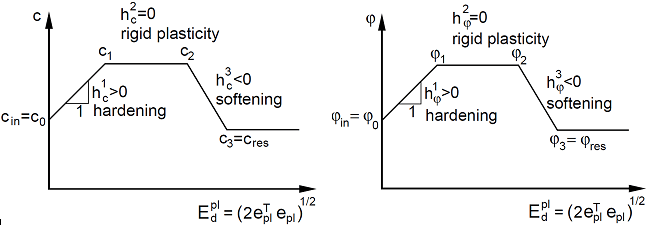 材料硬化和软化的分段线性函数:等效塑性偏应变Edpl a) 和粘聚力的函数关系 b) 和内摩擦角的函数关系
材料硬化和软化的分段线性函数:等效塑性偏应变Edpl a) 和粘聚力的函数关系 b) 和内摩擦角的函数关系
假设剪胀角ψ是恒定的,或者是内摩擦角φ的函数(Rowes剪胀理论),如下式
![]()
其中φcv是土体临界状态(土体塑性体积应变为零时的状态)时的恒定体积内摩擦角。为了防止剪胀角的无限增大(塑性体积张应变的增加),剪胀角必须设置界限值。例如,可以设置最大孔隙比emax,该参数对于给定的材料也适用。Rowes剪胀理论需要设置以下参数:
φcv | - | 临界状态内摩擦角 [-] |
e0 | - | 初始孔隙比 |
emax | - | 最大孔隙比 [-] |
当前孔隙比e可以用含当前体积应变εv和初始孔隙比e0的表达式表示:
![]()
![]()
其中: | e | - | 当前孔隙比 |
e0 | - | 初始孔隙比 | |
εv | - | 总体积应变 |
当当前孔隙比e超过最大孔隙比emax时,剪胀角ψ变为0。