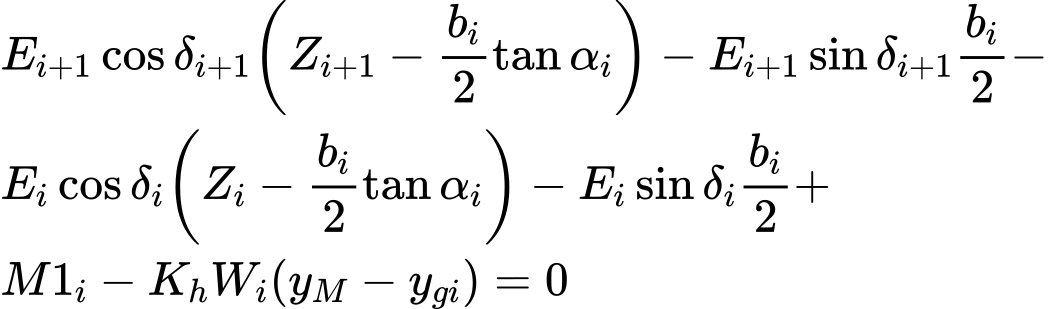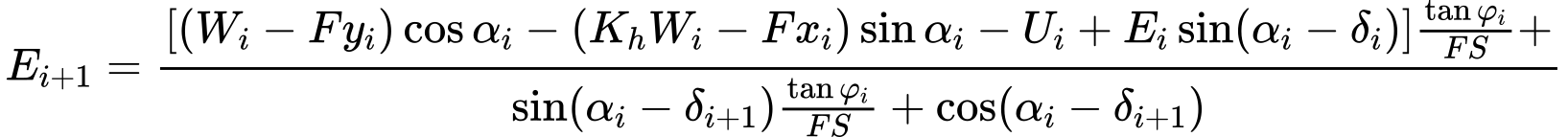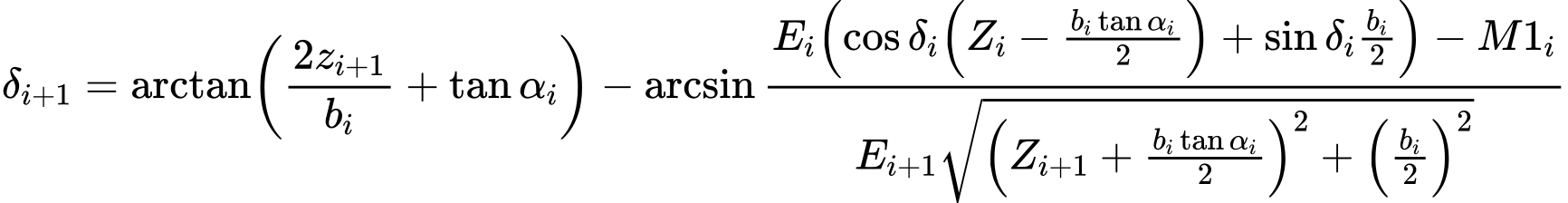Janbu
El método Janbu es un método general de cortes realizados en la base del equilibrio límite. Debe satisfacer el equilibrio de fuerzas y momentos actuando en bloques individuales (El único que no se satisface es el momento de equilibrio en el último bloque superior). Los bloques son creados dividiendo el suelo sobre la superficie terrestre dividiendo planos. Las fuerzas actuando en bloques individuales se muestran en la siguiente figura.
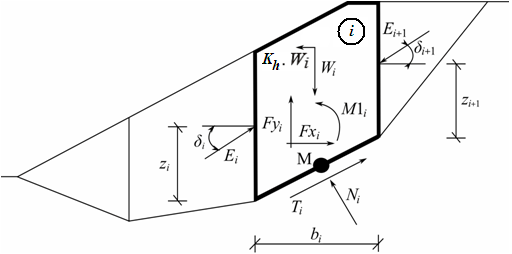Esquema estático – Método Janbu
Cada bloque se asume para contribuir a las siguientes fuerzas:
Wi | - | Peso del bloque, incluyendo material de sobrecarga que tenga el carácter del peso incluyendo la influencia del coeficiente vertical de sismoKv |
Kh*Wi | - | Fuerza de inercia horizontal que representa el efecto del sismo Kh, es el factor de la aceleración horizontal durante el sismo |
Ni | - | Fuerza normal en la superficie de deslizamiento |
Ti | - | Fuerza de corte en la superficie de deslizamiento |
Ei ,Ei+1 | - | Fuerzas ejercidas por cuerpos vecinos, inclinados desde el plano horizontal por el ángulo δi, resp. δi+1, y yacen a la altura zi, resp. zi+1, sobre la superficie de deslizamiento |
Fxi,Fyi | - | Otras fuerzas horizontales y verticales actuando en el bloque |
M1i | - | Momento desde las fuerzas Fxi, Fyi rotando sobre un punto M, el cuál es el centro del segmento de la superficie ith |
Ui | - | Presión de poro resultante en el segmento de la superficie ith |
Los siguientes supuestos se introducen en el método Janbu para calcular el límite de equilibrio de las fuerzas y momento de los bloques individuales:
- Los planos divididos entre bloques son siempre verticales
- La línea de acción de peso del bloque Wi pasa por el centro del segmento ith de la superficie de deslizamiento representada por el punto M
- La fuerza normal Ni actúa en el centro del segmento i-th de la superficie de deslizamiento, en el punto M
- La posición zi de la fuerza Ei actuando entre bloques, se asume en la superficie de deslizamiento en el punto extremo como z = 0
La elección de la posición zi puede ser una influencia significativa en la convergencia del método. Si se toma una mala suposición de la posición zi para una superficie dada, puede ser imposible satisfacer las condiciones de equilibrio (el algoritmo puede no converger). Las alturas zi sobre la superficie de deslizamiento se establecen aproximadamente a un tercio de la altura de la interfaz entre bloques. En caso de que no se satisfagan el algoritmo de condiciones de equilibrio, cambiar la altura a una posición diferente, ejemplo: ligeramente superior en la posición pasiva, cerca de la punta, mas bajo en la zona activa, cerca de la cresta de la pendiente.
La solución adopta la siguiente expresión:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Ecuación (1) representa la relación entre los valores de la tensión efectiva y total de la fuerza normal actuando en la superficie de deslizamiento. Ecuación (2) corresponde a las condiciones Mohr-Coulomb representando la relación entre la fuerza normal y la fuerza de corte en un segmento dado de la superficie de deslizamiento. Ecuación (3) representa la ecuación de la fuerza de equilibrio en dirección a la normal al segmento ith en la superficie de deslizamiento. Mientras que la ecuación (4) representa el equilibrio a lo largo del segmento i–th en la superficie de deslizamiento. SF es el factor de seguridad, el cual es utilizado para reducir los parámetros del suelo. Ecuación (5) corresponde a la ecuación de momento de equilibrio sobre el punto M, donde ygi es la coordenada vertical en el punto de aplicación del peso del bloque y yM es la coordinada vertical del punto M.
Modificando la fuerza de equilibrio de la ecuación (3) y (4) se obtiene la siguiente fórmula recursiva (6):
| (6) |
Este fórmula permite calcular todas las fuerzas Ei actuando entre los bloques para un valor dado de δi y SF. Esta solución asume que en el origen de la superficie de deslizamiento el valor E es conocido e igual a Ei = 0.
La fórmula para calcular los ángulos δi (7) proviene de la ecuación de equilibrio (5) como:
| (7) |
Esta fórmula permite el cálculo para un valor dado de δ todos los brazos de z de fuerzas actuando entre bloques, conociendo el valore izquierdo en una superficie de deslizamiento original, donde Z1 = 0.
El factor de seguridad SF es determinado empleando el siguiente proceso de interacción:
- Los valores iniciales de los ángulos se establecen como δi = 0 y las posiciones zi aproximadamente a un tercio de la atura de la interfaz.
- El factor de seguridad SF para un valor de δi dado, surge de la ecuación (6), mientras se asume el valor de En+1 = 0 en el extremo de la superficie de deslizamiento.
- Los valores de δi son proporcionados por la ecuación (7) utilizando los valores de Ei determinados en el paso previo.
- Los pasos 2 y 3 se repiten hasta que el valor de SF no cambia.
Es necesario evadir las soluciones inestables para que el proceso de iteración sea exitoso. Estas inestabilidades ocurren cuando toma lugar la división por cero en la expresión (6) ejemplo:
Otra comprobación para prevenir inestabilidad numérica es la verificación de parámetros mα – se satisface siguiendo las siguiente condición.
Por lo tanto, antes de ejecutar la iteración es necesario encontrar el valor crítico mas alto de SFmin que satisfaga las condiciones antes mencionadas. Los valores por debajo de éste valor crítico SFmin se encuentran en un área de solución inestable, por lo que la iteración comienza estableciendo SF a un valor por encima de SFmin y todos los valores resultantes de SF de las iteraciones ejecutadas son mayores a SFmin.
Generalmente los métodos rigurosos convergen mejor que los métodos simples (Bishop, Fellenius). Ejemplos con problemas convergentes incluyen dos secciones de superficie de deslizamiento empinada, geometría compleja, salto significativo en sobrecargas etc. Si no se obtiene resultado, recomendamos un pequeño cambio en los datos de entrada, ejemplo: superficie de deslizamiento menos empinada, ingreso de más puntos dentro de la superficie de deslizamiento, etc. o utilizar alguno de los métodos simples.
Bibliografía:
Janbu, N. 1954. Application of Composite Slip Surface for Stability Analysis. European Conference on Stability Analysis, Stockholm, Sweden.
Janbu, N. 1973. Slope Stability Computations. Embankment Dam Engineering - Casagrande Volume, R.C. Hirschfeld and S.J. Poulos, eds., John Wiley and Sons, New York, pp 47-86.