Empuxo Passivo - Teoria de Sokolovski
O empuxo passivo é dado pela seguinte expressão:
![]()
onde: | Kpg | - | coeficiente de empuxo passivo para solos não coesivos |
Kpc | - | coeficiente de empuxo passivo devido à coesão | |
Kpp | - | coeficiente de empuxo passivo devido a sobrecargas | |
σz | - | tensão vertical geostática |
Neste método são consideradas expressões individuais para determinar a magnitude do empuxo passivo e a superfície de deslizamento; a Figura seguinte mostra as variáveis a considerar:
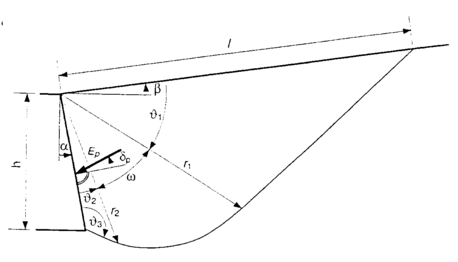 Empuxo passivo na superfície de deslizamento segundo Sokolovski
Empuxo passivo na superfície de deslizamento segundo Sokolovski
Ângulos que definem a superfície de deslizamento:
![]()
![]()
![]()
![]()
![]()
![]()
onde: | φ | - | ângulo de atrito interno do solo |
δp | - | ||
β | - | inclinação do talude |
Vetor rádio da superfície de deslizamento:
![]()
![]()
![]()
Considerando ω < 0 , o limite de ambas as zonas r1 e r2 é numericamente sobreposto, o que resulta no desenvolvimento da superfície de deslizamento numa zona de sobreposição. Os coeficientes de empuxo passivo Kpg, Kpp, Kpc são dados por:
![]()
![]()
![]()
onde: | φ | - | ângulo de atrito interno do solo |
δp | - | ||
α | - | inclinação da parede da estrutura |
![]()
Variáveis auxiliares: ipg, ipp, ipc, gpg, gpp, gpc, tpg, tpp, tpc
para: | | |
| | |
| | |
| | |
| |
![]()
onde:
![]()
As seguintes expressões são utilizadas para determinar os coeficientes de empuxo passivo em solos com o ângulo de atrito interno nulo:
![]()
![]()
onde:
![]()
![]()
![]()
![]()
Bibliografia:
Sokolovski, V.V., 1960. Statics of Soil Media,Butterworth, London.